Лекция 7. Дискретные случайные величины

В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Среди случайных величин выделяют дискретные и непрерывные случайные величины.

Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным.

Примеры дискретной случайной величины: запись показаний спидометра или измерений температуры в конкретные моменты времени.

Случайные величины обозначают прописными буквами латинского алфавита X, Y, Z,..., а значения, которые они принимают, - соответственно строчными: x,y,...

Правило, устанавливающее связь между значением СВ и ее вероятностью, называется законом распределения СВ.

Например, ДСВ X представляет собой конечный (или бесконечный) ряд чисел $x_1, x_2, x_3, ...x_n, ...$. Если заданы вероятности $p_1, p_2, p_3, ...p_n, ...$, то его называют рядом распределений. Обычно закон распределения ДСВ задается в виде таблицы, в первой строке которой расположены значения ДСВ, во второй - соответствующие им вероятности.

При этом сумма вероятностей всех возможных значений ДСВ равна 1:

$\textstyle\sum_{i=1}^n p_i=1$

Задача 1.

В результате подбрасывания двух игральных костей появляется некоторое число X – случайная величина, характеризующая сумму выпавших очков с определенной вероятностью. Найдите закон распределения случайной величины X. Величина Х может принимать значения от 2 до 12

ДСВ считается заданной, если указан закон ее распределения, т.е. известны все значения ДСВ и вероятность каждого из них.

Математические законы теории вероятностей получены в результате обобщения закономерностей массовых явлений природы и общества. Под массовостью в данном случае понимается значительное число повторяющихся испытаний в одинаковых или сходных условиях. При изучении массовых явлений особую роль играет группа теорем, известная в математике под названием закон больших чисел.

Благодаря этим теоремам, устанавливаются закономерности, возникшие в результате наложения большого числа случайных факторов. Так, одной из установленных закономерностей СВ является предсказуемость результатов: при определенных условиях СВ начинает вести себя не как случайная. При суммировании большого числа случайных величин закон распределения их суммы при соблюдении ряда условий близок к нормальному.

С другой стороны, под законом больших чисел понимают давно установленное (наблюдаемое) свойство устойчивости массовых случайных явлений, смысл которого в том, что средний результат действия большого числа случайных явлений становится практически неслучайным, т.е. может быть достаточно точно предсказан. Благодаря закону больших чисел появляется возможность делать научные прогнозы случайных явлений с достаточно высокой точностью, а также оценивать точность этих прогнозов.

Особую роль играют различные формы центральной предельной теоремы, так как устанавливают условия возникновения нормального закона распределения.

Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

• отклонение при стрельбе;
• погрешности измерений (однако погрешности некоторых измерительных приборов имеют иное распределение);
• некоторые характеристики живых организмов в популяции.

Поскольку каждому значению $х$ ДСВ ставится в соответствие ее вероятность, то закон распределения можно задавать с помощью функции распределения ДСВ.

Существуют разные законы распределения СВ: равномерное распределение, показательное, нормальное, биноминальное и т.д.

Функцией распределения $F(x)$ ДСВ $ξ$ называется вероятность события $ξ < х$:

$F(x) = Р(ξ < х)$.

Свойства функции распределения ДСВ:

1. Функция непрерывна при $x \not = x_i$ и имеет разрывы при $х = x_i$;
2. Функция распределения постоянна на полуинтервале $(x_i; x_{i+1}]$;
3. $F(x) = \textstyle\sum_{x_i < x}p_i$ - свойство накопительной вероятности.

$F(x)=\begin{cases} 0 &\text{при } x \leq x_1 \\ p_1 &\text{при } x_1 < x \leq x_2 \\ 1 &\text{при } x > x_2 \end{cases}$

График функции распределения произвольной ДСВ представляет собой «возрастающую ступеньку»

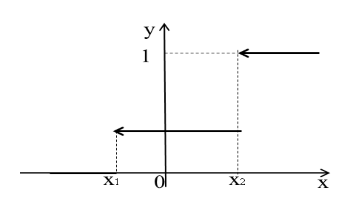
Задача 2.

Дискретная случайная величина задана рядом распределений:

Составьте функцию распределения и постройте ее график.

Решение. $F(x)=\begin{cases} 0 &\text{при } & x \leq -2 \\ 0,35 &\text{при } & -2 < x \leq 2 \\ 0,77 &\text{при } & 2 < x \leq 5 \\ 1 &\text{при } & x > 5 \end{cases}$

График функции

Задача 3.

В мастерской ремонтируют пять машин. Вероятность того, что любая из машин отремонтирована, равна 0,2. Случайная величина Х – число отремонтированных машин.

1. Cоставьте закон распределений ДСВ и постройте его график;
2. Cоставьте функцию распределения, постройте ее график.

Решение.

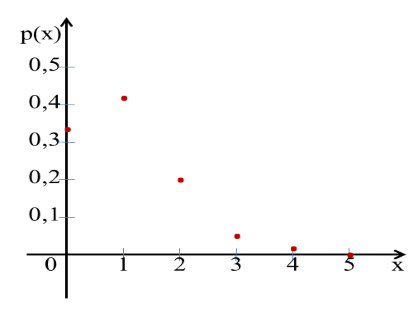
а) Число отремонтированных машин может быть: 0,1,2,3,4,5. Найдем вероятность каждого случая, используя формулу Бернулли.

$Р(0) = 0,8^5 =0,32768$

$Р(1) = C{1 \atop 5} · 0,2^1 · 0,8^4 = 5 · 0,2 · 0,4096 = 0,4096$

$Р(2) = C{2\atop 5} · 0,2^2 · 0,8^3 = 0,2048$

$Р(3) = C{3\atop 5} · 0,2^3 · 0,8^2 = 0,0512$

$Р(4) = C{4\atop 5} · 0,2^4 · 0,8^1 = 0,0064$

$Р(5) = 0,2^5 = 0,00032$

Составим закон распределений в виде ряда:

Построим график закона:

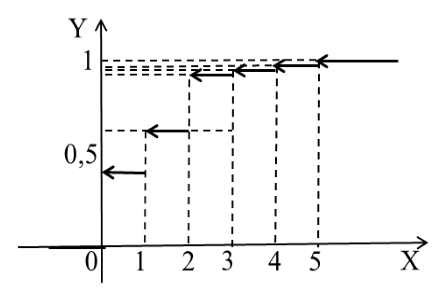
б) $F(x)=\begin{cases} 0 &\text{при } & x \leq 0 \\ 0,32768 &\text{при } & 0 < x \leq 1 \\ 0,73728 &\text{при } & 1 < x \leq 2 \\ 0,94208 &\text{при } & 2 < x \leq 3 \\ 0,99328 &\text{при } & 3 < x \leq 4 \\ 0,99968 &\text{при } & 4 < x \leq 5 \\ 1 &\text{при } & x > 5 \end{cases}$

График функции распределения имеет вид: