Лекция 9. Понятие непрерывной случайной величины

Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно.

Пример непрерывной случайной величины: запись показаний спидометра или измерений датчика температуры в течение конкретного интервала времени.

Результат эксперимента $\xi$ будем называть (СВ), если для любого $x ∈ R$ неравенство $\xi < x$ является событием, т.е. определена вероятность $Р(\xi < x)$. Эта вероятность как функция от х называется функцией распределения (ФР) случайной величины $\xi$ и обозначается $F(х)$.

Функцией распределения НСВ называют вероятность того, что случайная величина $\xi$ в результате испытания примет значение меньше $х$:

$F(х) = Р(\xi < х)$.

Свойства функции.

1. Функция распределения монотонно не убывает;
2. $\lim\limits_{x\to\infty}F(х) = 1$
3. $\lim\limits_{x\to -\infty}F(х) = 0$
4. Функция непрерывна слева при любом значении $х$;
5. Вероятность того, что случайная величина $\xi$ примет значение в полуинтервале [а; в), равна $P\{а \leq \xi < в\} = F(в) - F(а)$

Задача 1.

Случайная величина Х задана функцией распределения $F(x)$:

$F(x)=\begin{cases} 0 &\text{при } x \leq -1; \\ {3 \over 4}x +{3 \over 4} &\text{при } -1 < x \leq {1 \over 3}; \\ 1 &\text{при } x > {1 \over 3}. \end{cases}$

Найдите вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале $(0; {1 \over 3})$.

Решение.

Вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (a;b), равна приращению функции распределения на этом интервале:

$Р(a < x < b) = F(b) – F(a)$.

Отсюда $Р(0 < x < {1 \over 3}) = F({1 \over 3}) – F(0) = ({3 \over 4}·{1 \over 3}+{3 \over 4}) - ({3 \over 4}·0+{3 \over 4}) = {1 \over 4}$.

Ответ: ${1 \over 4}$.

Задача 2.

Случайная величина Х задана функцией распределения F(x):

$F(x)=\begin{cases} 0 &\text{при } x \leq -2; \\ {1 \over 2}x +{1 \over \pi} &\text{при } -2 < x \leq 2; \\ 1 &\text{при } x > 2. \end{cases}$

Найдите вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (-1; 1).

Предлагается решить самостоятельно.

Задача 3.

Случайная величина Х задана функцией распределения F(x):

$F(x)=\begin{cases} 0 &\text{при } x \leq 2; \\ 0,5x -1 &\text{при } 2 < x \leq 4; \\ 1 &\text{при } x > 4. \end{cases}$

Найдите вероятность того, что в результате испытания величина Х примет значение:

• а) меньше 0,2;
• б) меньше трех;
• в) не меньше трех;
• г) не меньше пяти.

Решение.

а) Так как при $x \leq 2$ функция $F(x) = 0$, то $F(0; 2) = 0$, т.е. $Р(x < 2) = 0$;

б) $Р(x < 3) = F(3) = 0,5·3 - 1 = 0,5$;

в) события $X ≥ 3$ и $X < 3$ противоположны, поэтому $Р(X ≥ 3) = 1 - Р(x < 3) = 1 - 0,5 = 0,5$;

г) сумма вероятностей противоположных событий равна 1. События $X ≥ 5$ и $X < 5$ противоположны. А т. к. при $x > 4$ $F(x) = 1$, то $Р(X ≥ 5) = 1 - Р(x < 5) = 1 - F(5) = 1 - 1 = 0$.

Определение.

Плотностью распределения НСВ называют первую производную от функции распределения: $f(x) = F'(x)$. Плотность обозначается $р(х)$, значит $F(х) = \textstyle\int_{-\infty}^xf(t)dt$ (несобственные интегралы в программу Элементы высшей математики не входят)

Задача 5.

Найдите плотность распределения функции. Постройте графики функции и плотности.

$F(x)=\begin{cases} 0 &\text{при } x \leq 3; \\ (x-3)^2 &\text{при } 3 < x \leq 4; \\ 1 &\text{при } x > 4. \end{cases}$

Решение.

$p(x) = F'(x)=\begin{cases} 0 &\text{при } x \leq 3; \\ 2x - 6 &\text{при } 3 < x \leq 4; \\ 0 &\text{при } x > 4. \end{cases}$

График функции $F(x)$

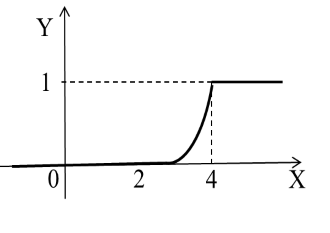
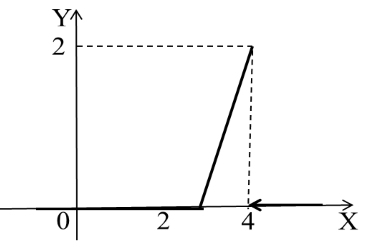
График плотности $p(x)$